We’ve all been in that place: you have a crazy geometry problem and are just missing that flash of insight necessary to solve it. While the situation may seem bleak, there is a way out, and that way is experimental math.

 

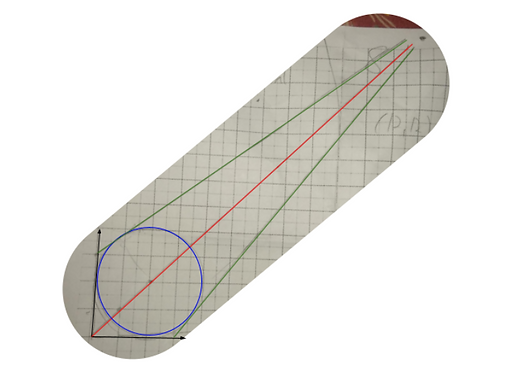
To illustrate experimental math, take the following example problem: There is a circle centered at (2, 2) with a radius of 2. A tangent is drawn from (3, 0). Where does this tangent intersect the line y = x? Wow, that seems difficult. It would take a lot of effort to get the tangent lines through these points manually, definitely much more time than would be available in a test or competition. 

 

Instead, why not try experimental math? Simply draw the circle, draw the tangent line, maybe even add another for the sake of symmetry, and find the point where it intersects y = x. According to the construction, it should be (12, 12). And what do you know? It works.

 

Of course, experimental math isn’t some sort of panacea. It can’t solve questions asking for proofs, and any non-integer (and not simple multiples of common non-integers like ½ and 2) answers should be approached with extreme caution, and it is always prone to user error.

 

Still, I’d highly recommend experimental math for any case where a general proof isn’t needed.

​