Distribution of Cakes

Fair distribution and Math…

Cutting cakes is very hard. And distributing a cake using mathematics is even harder. In the following, I will explain the math concepts involved in the fair distribution of cake, so on your next birthday, cutting a cake fairly won't be an issue anymore.

Image 1

Let’s first discuss the simplest situation, with two people and one cake.

We first define what we mean by fair. The definition of "fair" would be for each individual to get no less than 1n of the entire cake’s utility. However, this does not mean each individual gets the same amount of cake because different people have different tastes and preferences, and the utility resembled by each part of the cake is different. For example, one person may prefer strawberry topping over chocolate while another prefers chocolate over strawberry. For the first person, a piece of the cake with more strawberry topping with have higher utility while it would be the opposite for the other. 

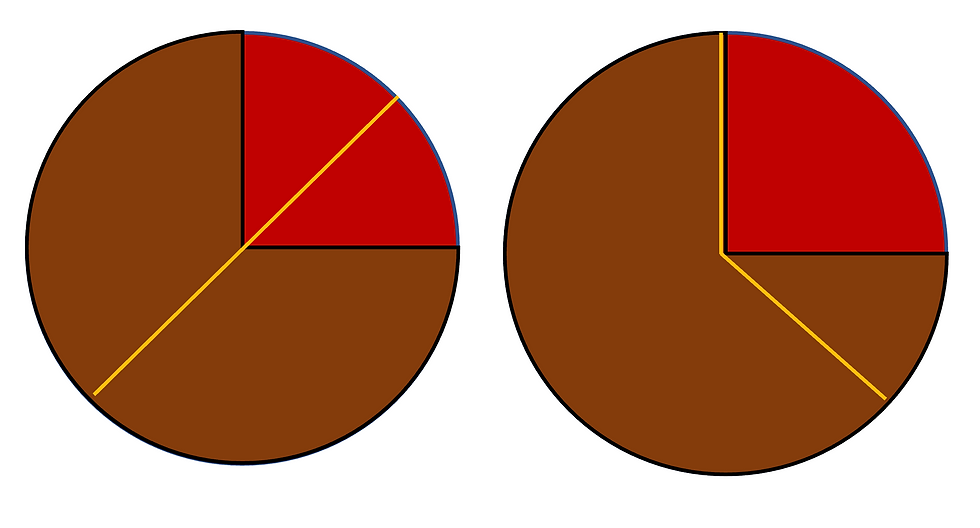
When splitting the cake, a method called “I cut; you choose” is used. One person would cut the cake, but the other person would choose first. Let’s name them A and B: A likes strawberries and B likes chocolate. When A cuts the cake, and let the yellow lines represent A’s cuts, the cake is split fairly in A’s view if the cake is cut as shown above. Because A likes strawberries, he can either distribute the same amount of chocolate and strawberries on each piece of the cake as seen in the graph on the left, or he can make one piece bigger while having more strawberries on the other piece, as seen in the graph on the right. 

The four parts shown on top have the same value to A, so no matter which one B chooses, A will always be guaranteed to get 50% of the entire cake’s value. Thus in A’s eyes, person B gets 50% of the cake’s value as well. As for person B, there is no way he can lose since he can always pick the piece that means more to him. In this case, he will either get one of the evenly distributed pieces or one with more chocolate. In his eyes, he either gains more of the cake’s value than A or gets the same value.

Image 2

Things gets a bit more complicated when three people get involved.

The way to distribute a cake among three is either kicking one person out of the room and split the cake among two or apply the following methods. 

Method 1 The moving Knife method

Have the cake as a rectangle so that it’s easier to visualize.  

After having the cake, let s person run the knife along the side of the cake. Whenever a person thinks the part, the knife moved along is already 13 of the cake, the person calls out and gets the part of cake. Then repeat the process of “I cut; you choose”. The first person, A, who thinks the part is already 13 of the cake will have to call out, or else he faces risk as another person, B, may claim the part, A values as 13 of a cake. If B claims the part, A and C has to split the cake among a piece which A values as less than 13 of the cake. 

However, this process may cause jealousy, as in A’s view, A will only get 13 of a cake, B may get ¼ due to the difference in tastes and preferences, but in that situation, C will get 512, an amount greater than A’s 13. Although the system is fair, in which everyone got ≥1n of the cake in their view, jealousy is bad. Thus we still need a better method.

Let one person among the party of three run the knife along the side of the cake. Whenever the other two think the knife has moved through a third of the cake, they call out and the person cutting the cake gets that part of the cake. Then repeat the process of “I cut; you choose”. The first person, A, who thinks the part is already a third of the cake will have to call out, or else he faces the risk of another person, B, claiming the bigger part. In the point of view of A, this piece of the cake is valued at a third of the total utility. If B claims the part, A and C has to split the cake among a piece which A values as less than a third of the cake. 

However, this process may cause jealousy, as in A’s view, A will only get 1/3 of a cake, and B may get 1/4 due to the difference in tastes and preferences, but in that situation, C will get 5/12, an amount greater than A’s 1/3. Although the system is fair, in which everyone got ≥1/n of the cake in their view, the method causes jealousy. Thus we still need a better method.

Method 2 is a more complicated form of “you cut; I choose”. Person A first cuts the cake, and then person B can choose whether to cut the piece even smaller or leave it. If B leaves the piece person A cuts, person A has to take the piece. If B cuts the piece, that person A had cut, even smaller, person C can choose whether to take the piece or not. Whatever happens, the person who cut the cake last has to take the piece if no one else took it. Person A would want to make the piece around his view of 1/3 the cake. Person B can cut the cake to B’s view of 1/3 a cake. Person C takes the cake if he also agrees it’s 1/3 of a cake. If a person cut the cake too small, person B can refuse to take the cake. If person B cuts the cake too small, person C can refuse to take the cake. Once someone took the piece of cake, the two people left can repeat the “you cut; I choose” process.

Image:

“Cutting Cake.” 01easylife, 01easylife.com/this-method-for-cutting-cake-is-raising-eyebrows.

Leone, Sergio, director. The Good, the Bad and the Ugly.