
Rudy Jatnieks '24
One Theorem Many Proofs: Isosceles Triangle Theorem
The isosceles triangle theorem states “If two sides of a triangle are congruent, then the angles opposite to these sides are congruent.” For a triangle to be isosceles, it must contain two sides of equal length. In order to prove this theorem, we must start with the isosceles triangle ∆ABC, where sides AC and BC are equal. The next step is to draw the bisector of ∠ACB. To prove that the “opposite angles” are congruent, we are going to prove that the ∆CAD and ∆CDB are congruent. With AC = AB given and ∠ACD = ∠BCD because ∠ACB, we can add CD = CD because they are the same segment in both triangles. These three pieces of information allow us to prove that the triangles are congruent through SAS, or “side-angle-side.” Hence, we can conclude ∠CAB = ∠CBA because every side and angle in congruent triangles are congruent. Additionally, we have ∠CDA = ∠CDB = 90˚.
Another example of an isosceles triangle theorem proof is through using SSS, or “side-side-side,” to prove that the opposite angles are congruent. Instead of starting with the angle bisector of ∠ACB, we add the midpoint of segment AB, point D. We then connect D to ∠ACB to form the two right triangles we formed before. However, now we know that segments AD and DB are congruent. Therefore, with AC = BC given and CD = CD because they are the same segment, we can conclude that the triangles are congruent because of SSS. And, as stated before, ∠CAB = ∠CBA because every side and angle in congruent triangles are congruent.
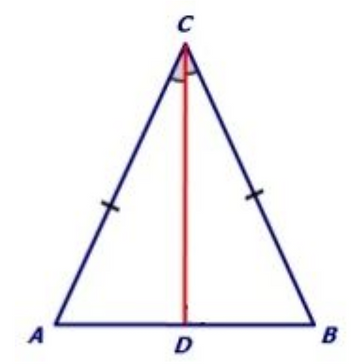
Finally, we can draw the height of ∆ABC to base AB and name the intersection on side AB as point D. Now, we can also use SSA to prove this theorem because AC > CD. AC = BC (given; CD is less than both AC and CB), CD = CD (same side), and ∠ADC = ∠BDC because they are both 90 degrees. This seems like an abundance of proofs available to prove just one theorem. In conclusion, the isosceles triangle theorem is a great example of showing how a theorem could have many different proofs.